H形鋼はコンクリート梁のような矩形断面ではなく、圧縮側、引張側にそれぞれフランジを持つ構造で、より少ない断面積で曲げ抵抗を大きくした鋼部材です。
そのため矩形コンクリートとは断面力の計算方法が異なります。
この記事を読むと、H鋼の部材照査式の意味を理解し、実務において現場条件ごとに適切に応用することができるようになります。
軸力と曲げを受ける部材の照査式
H形鋼で軸力と曲げを同時に受ける場合、道路土工仮設構造物工指針(平成11年)では、次式の通り応力照査を行うよう記載されています。
$$(照査式1):\frac{σ_c}{σ_{caz}}+\frac{σ_{bcy}}{σ_{bagy}(1-\frac{σ_c}{σ_{eay}})}+\frac{σ_{bcz}}{σ_{bao}(1-\frac{σ_c}{σ_{eaz}})}≦1$$
$$(照査式2):σ_c+\frac{σ_{bcy}}{(1-\frac{σ_c}{σ_{eay}})}+\frac{σ_{bcz}}{(1-\frac{σ_c}{σ_{eaz}})}≦σ_{cal}$$
各記号の意味
公式中の記号の意味をご紹介します。
\(σ_c\):照査する断面に作用する軸方向力による圧縮応力度\((N/mm^2)\)
\(σ_{bcy},σ_{bcz}\):それぞれ強軸および弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度\((N/mm^2)\)
\(σ_{caz}\):弱軸まわりの許容軸方向圧縮応力度\((N/mm^2)\)。次式で計算。

\(σ_{bagy}\):局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度\((N/mm^2)\)。次式で計算。

\(σ_{bao}\):局部座屈を考慮しない許容曲げ圧縮応力度の上限値で、\(210(N/mm^2)\)。
\(σ_{cal}\):圧縮応力を受ける自由突出板(=フランジ)の局部座屈に対する許容圧縮応力度で、\(210(N/mm^2)\)。
\(σ_{eay},σ_{eaz}\):それぞれ強軸・弱軸まわりのオイラー座屈応力度\((N/mm^2)\)。次式で計算。

照査式の意味を理解しよう
照査式1はH形鋼全体の座屈を考えたもので、照査式2はフランジの局部座屈を考慮した式です。
この記事では、照査式1、2の意味とメカニズムを順に解説していきます。
照査式1の意味
照査式1は、外力に対して、H鋼が全体座屈しないかを照査するための式です。
$$(照査式1):\frac{σ_c}{σ_{caz}}+\frac{σ_{bcy}}{σ_{bagy}(1-\frac{σ_c}{σ_{eay}})}+\frac{σ_{bcz}}{σ_{bao}(1-\frac{σ_c}{σ_{eaz}})}≦1$$
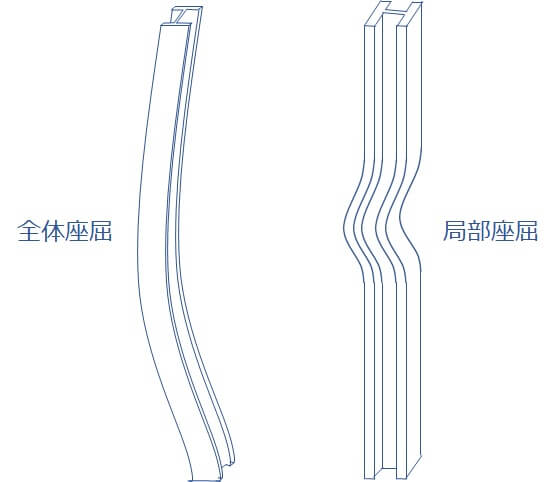
全体座屈とは、下図のようにH鋼を棒部材として見たときに発生する座屈のことです。
大学で習った柱の座屈と同じメカニズムで発生する座屈と同じと考えれば分かりやすいです。
ちなみに局部座屈とは、フランジが局所的に座屈するような座屈形態を指します。
左辺第一項
左辺第一項\(\frac{σ_c}{σ_{caz}}\)は、軸方向圧縮応力を弱軸まわりの許容軸圧縮応力度で除したもので、単純に軸方向圧縮に対する座屈照査項です。
左辺第二項
左辺第二項\(\frac{σ_{bcy}}{σ_{bagy}(1-\frac{σ_c}{σ_{eay}})}\)は、強軸まわりの曲げ座屈に対する照査項です。
①曲げモーメントによる曲げ圧縮応力を強軸まわりの全体座屈に対する許容値で除したもの(\(\frac{σ_{bcy}}{σ_{bagy}}\))があり、②それを、オイラー座屈応力度に対する軸方向圧縮力の比を用いた\((1-\frac{σ_c}{σ_{eay}})\)で除しています。
①は、曲げモーメントによる曲げ応力の、全体座屈に対する許容度を計算するものです。
②は、軸方向圧縮力による座屈度であり、1から引いたものの逆数(\(\frac{1}{(1-\frac{σ_c}{σ_{eay}})}\))は、軸力による座屈が大きいほどに大きな値になります。
よって、項全体としては(曲げによる座屈しやすさ)×(軸力による座屈しやすさ)を表しています。
左辺第三項
左辺第三項\(\frac{σ_{bcz}}{σ_{bao}(1-\frac{σ_c}{σ_{eaz}})}\)は、第二項と同様に曲げによる座屈照査ですが、第二項が強軸まわりなのに対し、第三項は弱軸まわりの曲げ座屈照査項という違いがあります。
以上のような左辺の値が右辺(=1)よりも小さければ、座屈を促すが外力要素よりも部材の許容値が大きいということで、全体座屈に対して安全だと言えるわけです。
照査式2の意味
照査式2は、H鋼のフランジが局部座屈しないかを照査するための式です。
$$(照査式2):σ_c+\frac{σ_{bcy}}{(1-\frac{σ_c}{σ_{eay}})}+\frac{σ_{bcz}}{(1-\frac{σ_c}{σ_{eaz}})}≦σ_{cal}$$
H鋼全体として外力に抵抗できる大きさは、部材全体における最小の抵抗力となります。
局所的な脆弱部が発生すると、最小抵抗力が小さくなるため、局所的でも結果として全体の強度を弱めることになるのです。
ではさっそく各項の意味を理解していきましょう。
照査式2は、左辺に作用力項群、右辺に許容値が用意された構造となっています。
左辺第一項
第一項\(σ_c\)は、軸方向力による圧縮応力度であり、座屈を促す軸方向応力を表します。
左辺第二項
第二項\(\frac{σ_{bcy}}{(1-\frac{σ_c}{σ_{eay}})}\)は、強軸まわりについて、座屈を促す曲げ圧縮応力を、軸力とオイラー座屈応力度との商から求めた軸力による座屈促進度を掛けたものです。
照査式1における\(σ_{bagy}\)の役割が右辺(\(σ_{cal}\))に移っているものと考えればよいです。
左辺第三項
第三項\(\frac{σ_{bcz}}{(1-\frac{σ_c}{σ_{eaz}})}\)は、第二項と同様のものを弱軸まわりについて計算するものです。
以上の三項の和が、右辺=自由突出板(=フランジ)の局部座屈に対する許容応力度\(σ_{cal}\)以下であることを確認することで、安全を照査しています。
留意点
ねじれ座屈も要検討
H鋼の座屈として、雑巾絞りのようにねじれながら座屈する「ねじれ座屈」と呼ばれる座屈形態があり、施工条件や荷重条件によってはこちらも検討する必要がありますので、そういう座屈もあるんだと存在だけでも認知しておくとよいです。
公式の適用範囲
この記事で紹介した軸力と曲げを受ける部材の照査公式ですが、許容値が\(210(N/mm^2)\)と与えられているのは、同式がSS400の鋼材を対象としているためです。
SM490の鋼材を用いる場合には許容値は\(280(N/mm^2)\)ですので、公式の適用範囲外となります。
また、同式は道路土工仮説構造物工指針に記載された公式であり、安全率1.5を用いた仮説構造物を対象としています。
本設構造物の場合には、例えばSS400の許容応力度が\(210(N/mm^2)\)ではなく\(140(N/mm^2)\)となり、こちらも公式の適用範囲外ですのでご注意ください。
以上、軸方向圧縮力と曲げモーメントを同時に受ける部材の照査方法について解説しました。
軸力と曲げを同時に受けるH鋼部材の照査は、土留支保工としての切梁や腹起しなど頻繁に計算機会が訪れますので、ぜひ抑えておいてください。

