土留め壁の弾塑性解析では、切梁をバネとしてモデル化することで土留め壁の応力・たわみを算出できます。
火打ち梁も切梁と同様にバネとしてモデル化されますが、土留め壁に対して斜めに設置される火打ち梁のばね定数を計算する方法は少し変わっています。
この記事では火打ち梁のばね定数を計算する方法を導出から詳しく解説します。
弾塑性解析のメカニズム
土留壁や土留め支保工の仕様を決めるための土留め弾塑性解析では、断面モデルにおける力のつり合いによって土留壁や支保工の応力計算・変位量計算を行います。
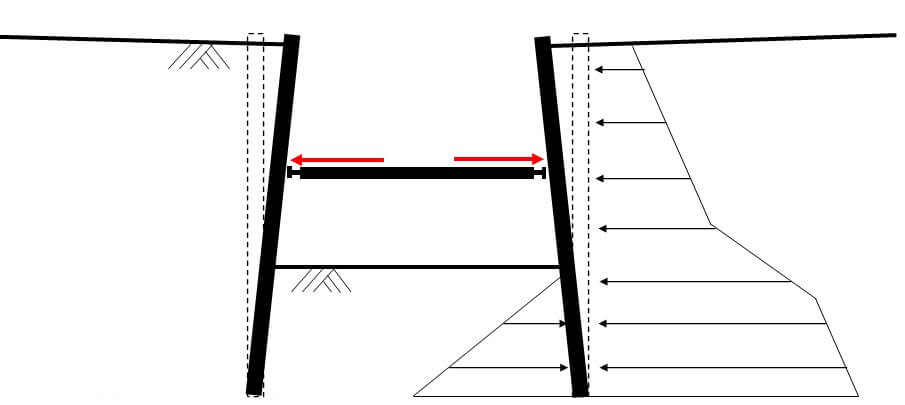
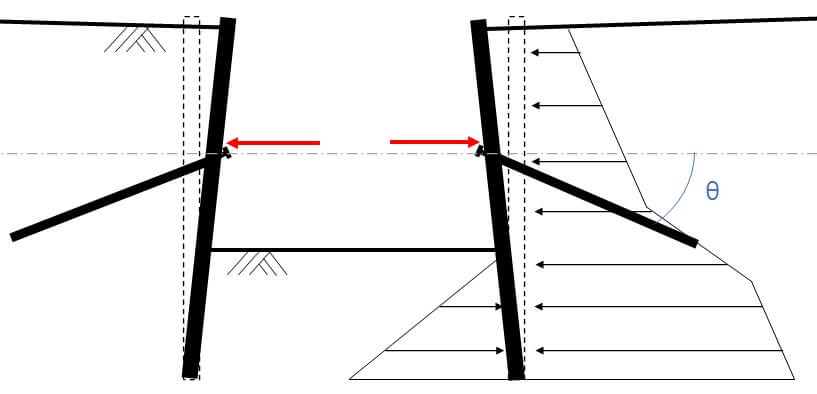
下図のように、右の土留壁には背面側から主働土圧が作用して土留め壁に微小な左向きの変位を与えます。これにより、掘削側には床付け以深に受働土圧が発生します。また、切梁は主働土圧により縮むバネのような挙動となり、切梁バネ反力が発生します。
土留め壁の変形に応じて受働土圧や切梁反力が変化し、力がつり合う位置まで土留め壁が変形します。これを使って土留め壁に発生する応力や変形を計算するのが弾塑性解析です。
切梁のバネ定数の計算方法をおさらい
まずは切梁バネのばね値の計算方法をおさらいしておきます。
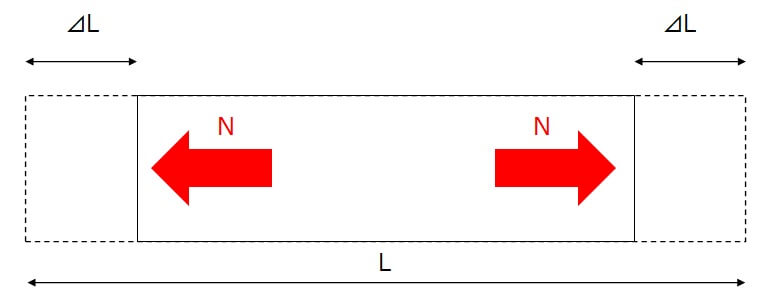
切梁のばね値は、次式で計算できます。
$$k=\frac{2αEA}{L}$$
ここで、\(α\):切梁のゆるみ係数(一般にジャッキを取り付けてゆるみをなくすため\(α=1.0\))、\(E\):切梁部材のヤング係数、\(A\):切梁部材の断面積、\(L\):切梁の長さ
切梁中央は移動が無い点、つまり不動点です。切梁の片側半分のみについて見ると、長さ\(\frac{L}{2}\)だったのが、\(⊿L\)だけ縮んでいます。
一方、応力とひずみ関係式から、
$$σ=Eε$$
$$N/A=E\frac{⊿L}{(L/2)}$$
フックの法則より、\(N=k⊿L\)だから、
$$k/A=E\frac{1}{(L/2)}$$
$$\therefore k=\frac{EA}{(L/2)}$$
これにゆるみ係数\(α\)を与えると切梁のバネ算出公式\(k=\frac{2αEA}{L}\)を導出できる。
しかし、これは切梁が土留壁に対して垂直に掛かっていてこその式であり、角度をつけて設置される火打ちの場合には適用できない式です。
火打ちのばね定数の導出
火打ちばねの構造を図解することで火打ちのばね値計算式を導出していきます。
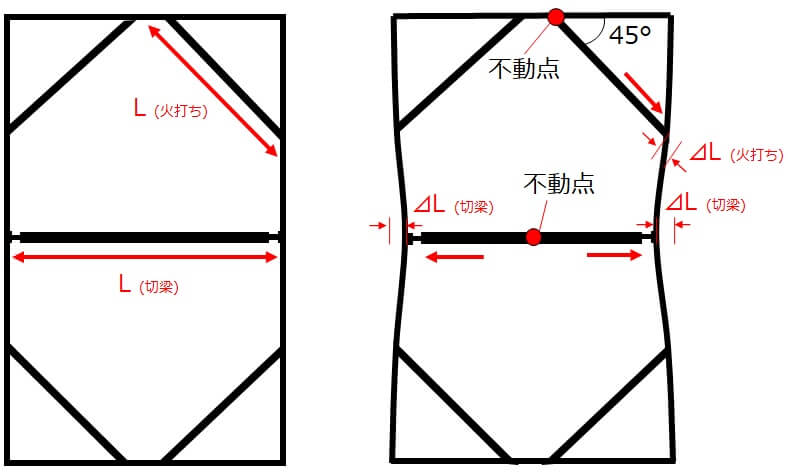
火打ちバネと切梁バネの違いは、①不動点の位置、②土圧に対して角度を持っていること、の2点です。
①まず、切梁は左右から均等に土圧を受けるため、不動点は切梁中央にありましたが、火打ちの場合、左右に1つずつ火打ちが配置されており、片側の土圧のみに機能することから、火打ちの不動点は端部にあります。
つまり、火打ちのバネ値を考えるときの長さLは、切梁のときのようにL/2を使うことはせず、火打ちの長さLをそのまま使います。
②次に、土圧に対して角度を持っている件についてですが、これは斜め部材の力のつり合いについて考えることで解決します。力のつり合いは下図の通りです。
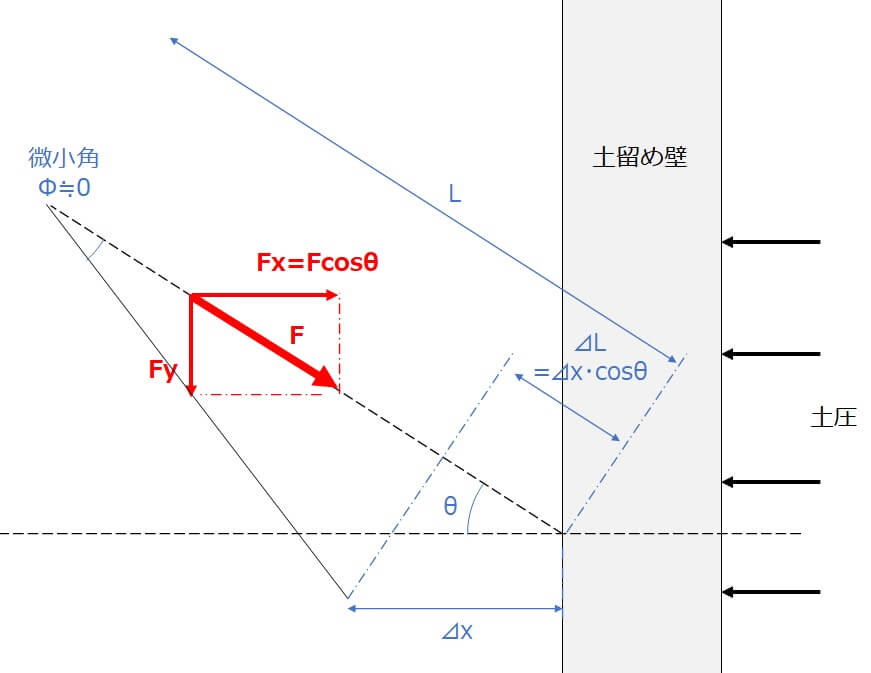
最終的に求めたいのは「土留め壁がいくら変形したときに、いくらのバネ反力が発生するのか」です。
土圧を受けて土留め壁が変形し、火打ちも⊿Lだけ縮みました。このとき発生するバネ反力をFとします。
部材方向について見ると、長さ⊿L=⊿x・cosθだけ縮み、バネ反力Fが発生しています。前述の切梁バネ値と同様にして応力ひずみ関係式から、
$$F/A=E\frac{⊿xcosθ}{L}$$
$$F=EA\frac{⊿xcosθ}{L}$$
ここで、Fは火打ち方向のバネ反力です。土留めの弾塑性計算では、x方向(土圧方向)について計算を解いていきますので、x方向成分\(Fx=Fcosθ\)を使います。
$$Fx=Fcosθ=EA\frac{⊿x(cosθ)^2}{L}$$
$$k⊿x=EA\frac{⊿x(cosθ)^2}{L}$$
$$\therefore k=\frac{EA(cosθ)^2}{L}$$
切梁と同様に、これにゆるみ係数\(α\)が乗りますので、最終的には次式によって火打ちバネのばね定数を計算できます。
$$k=\frac{αEA(cosθ)^2}{L}$$
すなわち、斜めに設置されたバネ部材は、切梁のバネ値計算式に\((cosθ)^2\)を乗ずることで計算できるわけです。
火打ちは平面的な斜め部材ですが、土留めアンカーのように鉛直面に斜めの部材に対しても同式が適用できます。
土留めアンカーのバネ値計算
グラウンドアンカーを土留め支保工として用いる場合には、前述の式に水平線との角度θを用いることでバネ値を計算できます。
以上、今回は土留め壁に対して斜めに設置される火打ちバネのバネ定数の計算方法を紹介しました。

