皆さんは、2点の集中荷重が作用する単純梁は、2点荷重が中央に載荷される場合に曲げモーメントが最大だと勘違いしてはいませんか?
結論から言うと、中央から1:3の距離に2点荷重がそれぞれ載荷される場合に最大曲げモーメントが発生します。
この記事では、2つの集中荷重が作用する単純梁における曲げモーメント算出公式と、なぜそうなるのか、その導出を解説します。
最大曲げモーメント・載荷位置の算出公式
2つの集中荷重が作用する単純梁に発生する最大曲げモーメント\(M_A\)、そのときの荷重の載荷位置\(a\)は次式の通り計算できます。
※ここでは、2点の集中荷重値Pが同じ大きさ、2点間の距離dが一定の場合を仮定します。
$$M_A=\frac{P(L-\frac{d}{2})^2}{2L}$$
$$a=\frac{L}{2}-\frac{d}{4}$$
導出
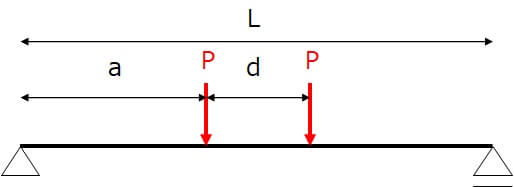
ここでは、2点荷重の値が同じ大きさ、2点間の距離は一定の場合を仮定します。
実際、建設コンサルやゼネコンの実務でも、このような条件が多いです。
具体的には、路面覆工桁の仕様設計にあたっては、自動車荷重をT荷重(荷重値P=100kN、距離d=1.75mの2点荷重)として、その2点荷重が単純梁に与える影響が最も大きくなるための、車の走行位置を考えます。
1点荷重それぞれによる発生曲げモーメント
まず、単純梁の任意の位置に1点荷重が作用する場合を考えます。
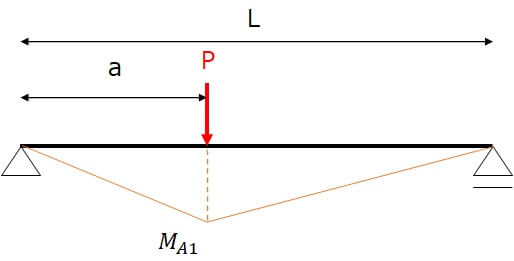
この場合、荷重作用位置Aに発生する曲げモーメントは次式の通りです。
$$M_{A1}=\frac{Pa(L-a)}{L} ・・・①$$
次に、2点目の荷重が単独で作用した場合を仮定し、その場合に上記と同じ位置に発生する曲げモーメントを考えます。
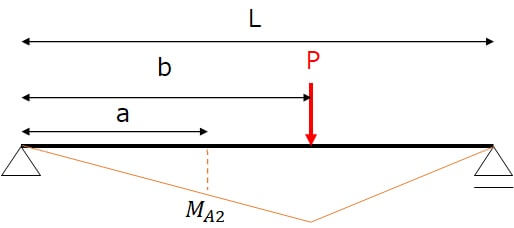
点Aに発生する曲げモーメントは次式で計算できます。
$$M_{A2}=\frac{Pa(L-b)}{L} ・・・②$$
2点荷重の重ね合わせ
前項で求めた2式は、それぞれの集中荷重によって同じ位置に発生する曲げモーメントを表しています。
曲げモーメントの重ね合わせの原理は、単純な和で計算できますので、2点間の距離の条件を追加した上で重ね合わせていきます。
まず、式②に対して、2点間の距離d(m)という条件を追加すると、\(b=a+d\)となり、次式のようになります。
$$M_{A2}=\frac{Pa\{L-(a+d)\}}{L}$$
これを式①重ね合わせると、
$$M_A=M_{A1}+M_{A2}$$
$$=\frac{Pa(L-a)}{L}+\frac{Pa\{L-(a+d)\}}{L}$$
$$=\frac{Pa}{L}\left[(L-a)+\{L-(a+d)\}\right]$$
$$=\frac{Pa(2L-2a-d)}{L}$$
$$=\frac{P\{-2a^2+a(2L-d)\}}{L}$$
最大曲げモーメント発生位置を算出
\(M_A\)を微分することで、最大曲げモーメントを発生させるための載荷位置を求めます。
$$(M_A)’=\left[\frac{P\{-2a^2+a(2L-d)\}}{L}\right]’$$
$$=\frac{P}{L}(-4a+2L-d)$$
\(M_A\)がマイナスの二次関数であることから、\(M_A\)が極致を取るときに\(M_A\)が最大値を取ります。
したがって、
$$(M_A)’=\frac{P}{L}(-4a+2L-d)=0$$
$$-4a+2L-d=0$$
$$\therefore a=\frac{L}{2}-\frac{d}{4}$$
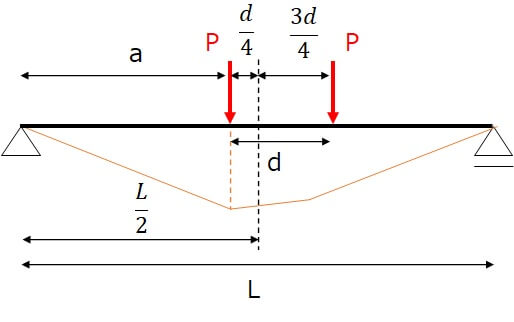
つまり、1点目の載荷位置aが、単純梁中央\((\frac{L}{2})\)から2点間距離dの\(\frac{1}{4}\)だけ離れた位置にあるときに最大曲げモーメントが発生します。
このときの荷重図は下図のようになっていて、梁中央に対して2点荷重が1:3の距離で載荷された場合に最大曲げモーメントが発生していることが分かります。
最大曲げモーメントの算出
2点荷重が1:3で作用する場合の最大曲げモーメントの値は、\(a=\frac{L}{2}-\frac{d}{4}\)を代入して次式で計算できます。
$$M_{A(\frac{L}{2}-\frac{d}{4})}$$
$$=\frac{P(\frac{L}{2}-\frac{d}{4})(2L-2(\frac{L}{2}-\frac{d}{4})-d)}{L}$$
$$=\frac{P(\frac{L}{2}-\frac{d}{4})(L-\frac{d}{2})}{L}$$
$$=\frac{P(L-\frac{d}{2})^2}{2L}$$
以上、今回は2つの集中荷重が作用する場合に、最大曲げモーメントを発生させる荷重載荷位置の計算方法をご紹介しました。

