この記事では、道路橋示方書に基づいた直接基礎の支持力計算について解説していきます。
そもそも直接基礎とは
直接基礎とは、べた基礎やケーソン基礎、クレーン接地等、地表面で直接荷重を支持する基礎、もしくは根入れ長が5m以内の比較的根入れ長が浅い基礎を指します。
ここで、根入れ土層は良質な支持層である必要があり、支持層の土質の目安や必要根入れ長については後述します。
直接基礎の支持力公式
直接基礎の許容支持力は、次式で計算できます。
$$Q_u=\frac{1}{n}Ae\{ακcN_cS_c +κqN_qS_q+\frac{1}{2}γ_1βB_eN_γS_γ\}$$
左辺の\(Q_u\)は許容支持力(kN)です。
安全率を設定する理由
支持力公式の右辺の先頭にある\(\frac{1}{n}\)を除く部分は「極限支持力」と呼ばれ、地盤が極限状態(破壊する状態)になる荷重値を表しています。
すなわち、地盤が究極的に保有している支持力ということです。
しかし、設計段階でこれを支持力としてみなして設計すると、万が一設計よりも若干外力が大きくなってしまった場合や施工誤差が生じた際に地盤が破壊してしまいます。
そこで、\(\frac{1}{n}\)をかけた(=安全率n(≧1)で割った)ものを許容支持力とすることで、極限支持力よりも小さい許容支持力に対して設計することにして、万が一の事故が起きないようにします。
単位面積あたりの許容支持力を計算したい
右辺の{}の外にある\(A_e\)は基礎の接地面積です。
応力に面積\(A_e\)をかけたものが左辺の許容支持力\(Q_u\)(kN)になっているという意味です。
両辺を\(A_e\)で割ってやれば\((kN/m^2)\)の単位を持つ「単位面積当たりの許容支持力」を得ることができます。
本題!右辺各項の解説
さて、ここからが本題です。
右辺の{}内の3つの項についてそれぞれ順に解説していきます。
地盤定数や上載荷重等の環境条件による3つの要素から支持力は計算できます。
1.地盤の粘着力による粘り支持力
2.根入れ地盤の拘束効果による支持力(上載荷重による支持力)
3.支持地盤の鉛直支持力
地盤の粘着力による粘り支持力
右辺第一項は地盤の粘着力が発揮する支持力を計算する項です。
$$(右辺第一項)=ακcN_cS_c$$
\(α\):基礎の形状係数
\(κ\):根入れ効果に対する割増係数
\(c\):基礎地盤の粘着力(kN/m2)
\(N_c\):荷重の傾斜を考慮した支持力係数
\(S_c\):支持力係数の寸法効果に関する補正係数
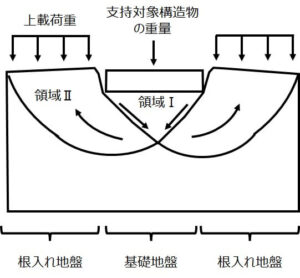
許容支持力式は、テルツァーギの支持力公式を拡張したものであり、その構造も下図(テルツァーギの支持力公式の考え方を示した図)を用いて説明することができます。
図のように基礎が微量の沈下を生じながら支持力を発揮し、上部構造物を支持することになります。
下図中の矢印ように、基礎が沈下すると、領域Ⅰは沈下し、それに伴い領域Ⅱを上方に押し上げます。
この動きに抵抗するのが基礎地盤の粘着力です。
右辺第一項はこの抵抗力を表しています。
沈下の動きを抑制する=支持する力というわけです。
根入れ地盤の拘束効果による支持力(上載荷重による支持力)
右辺第二項は根入れ地盤上の上載荷重及び根入れ地盤自重による支持力を計算する項です。
$$(右辺第二項)=κqN_qS_q$$
\(κ\):根入れ効果に対する割増係数
\(q\):根入れ地盤上の上載荷重及び根入れ地盤自重(kN/m2)
\(N_q\):荷重の傾斜を考慮した支持力係数
\(S_q\):支持力係数の寸法効果に関する補正係数
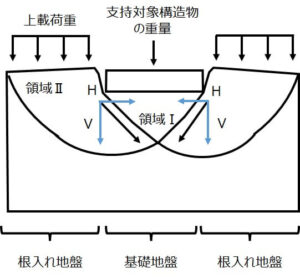
上載荷重は領域Ⅱの滑り力を増加させます。
滑り力は領域Ⅰを両側から挟み込むように拘束し、領域Ⅰの沈下に抵抗し、対象構造物を支持します。
ここで、支持力式におけるqの取り扱いですが、片側の上載荷重のみをqとして代入します。
図の通り、上載荷重の水平成分Hが両側で釣り合い、領域Ⅰを拘束しますので、基礎地盤を囲むように全方位に載荷されている必要があります。
支持力式への入力値としては、全方位に共通する最小の上載荷重とします。
支持地盤の鉛直支持力
右辺第三項は支持地盤のによる支持力を計算する項です。
第三項は基礎地盤が有する単純な支持力です。
$$(右辺第三項)= \frac{1}{2}γ_1βB_eN_γS_γ$$
\(γ_1\):支持地盤の単位体積重量(kN/m3)
\(β\):基礎の形状係数
\(B_e\):基礎の有効載荷幅(m)
\(N_γ\):荷重の傾斜を考慮した支持力係数
\(S_γ\):支持力係数の寸法効果に関する補正係数
良質な支持層の目安
直接基礎の根入れ効果は良質な支持層へ根入れしているときのみ考慮できます。
「良質な支持層」の目安は、砂質土であればN値30以上、粘性土であればN値20以上かつ圧密の恐れがない土層です。
支持層が弱い場合には地盤改良を施工することがありますが、現場で安定処理した改良強度は、同じ添加量の室内配合の強度よりも小さくなる傾向があることに注意が必要です。
必要な支持層の厚さ
前項の解説の通り、支持力公式中に支持層の厚さに関する項は存在しません。
では支持層の厚さがいくら以上あれば直接基礎の支持力公式を適用できるのでしょうか?
結論から言います。
直接基礎必要な支持層厚さは、一般的に基礎幅の2倍~3倍以上です。
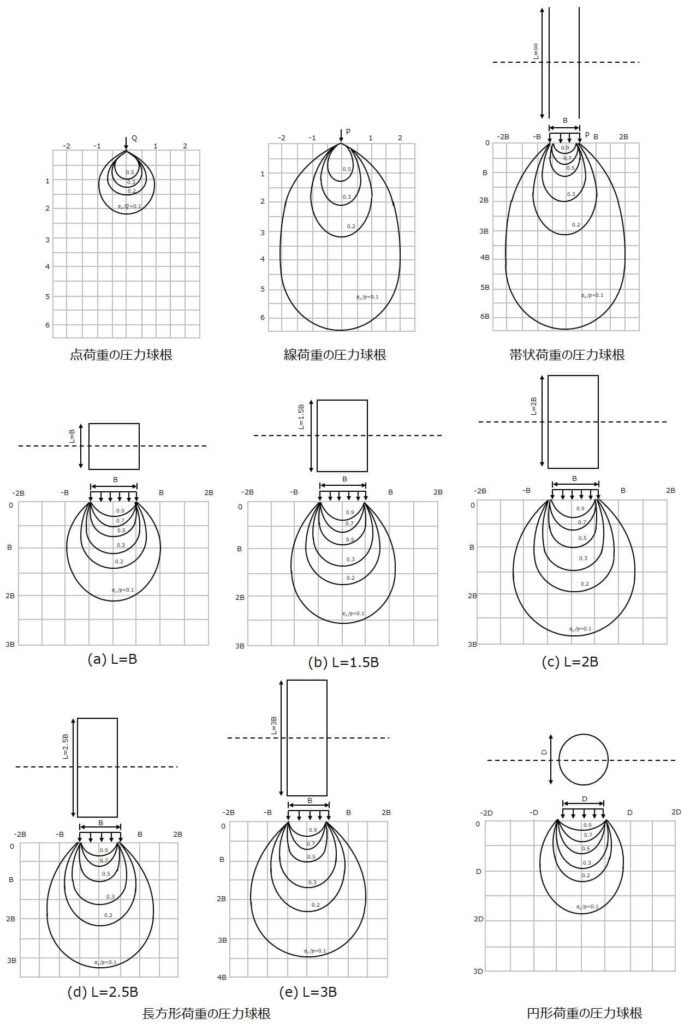
圧力球根図から、σ/p=0.1以上となる範囲(=上載荷重の1割以上の圧力がかかる範囲)を上載荷重の影響範囲とし、この範囲に支持層の存在が必要と考えます。
帯状基礎や円形基礎など基礎の形状によって変化しますので、以下の圧力球根図を参照してください。
各記号の算出方法
α, β:基礎の形状係数
\(α\)は1.0~1.3の範囲の値をとり、帯状の基礎であれば1.0、正方形や正円形であれば1.3となります。
それ以外の形状(長方形、楕円形、小判形)の基礎の場合は、\(1+0.3\frac{B_e}{D_e}\)で計算します。
ここで、\(B_e\)、\(D_e\)は基礎の有効幅であり、短い方が\(B_e\)と覚えておけば問題ありません。
基礎幅の比は縦断の細長さを表しており、これを用いて計算したαは基礎の形状係数と呼ばれます。
\(β\)も同様に、帯状基礎であれば1.0、正方形や円形であれば0.6、それ以外の場合は\(1-0.4\frac{B_e}{D_e}\)で計算します。
κ:根入れ効果の割増係数
\(κ\)は根入れ効果に対する割増係数と呼ばれる通り、根入れ長と基礎幅の比を用いて計算されます。
$$κ=1+0.3\frac{D’_f}{B_e}$$
ここで、\(D’_f\)は支持地盤もしくは支持地盤と同程度の良質な地盤への根入れ深さ(m)であることに注意が必要です。
一般に表層の地盤はn値2程度の軟弱な土質であることが多いです。
「N値2以下の粘性土では基礎との周面摩擦力がほぼゼロであり、支持性能は無視する」というのが、道路橋示方書含め多くの指針の記載されているところです。
つまり、表層の軟弱層に根入れしても十分な根入れ効果が得られませんので、\(D’_f =0\)とします。
ではどのような場合に根入れ効果の割増が可能なのでしょうか?
それは、表層の軟弱地盤対策として表層の地盤改良を施工した場合です。
地盤改良により人工的に強固な支持地盤を形成し、そこに直接基礎を根入れすることで、根入れ効果に対する割増係数κ≧1として支持力の割増を考慮することが可能になります。
\(N_c, N_q, N_γ\):基礎の傾斜にかかる係数
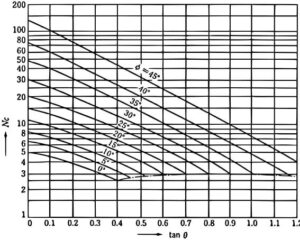
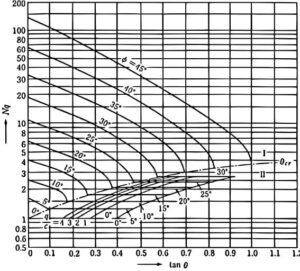
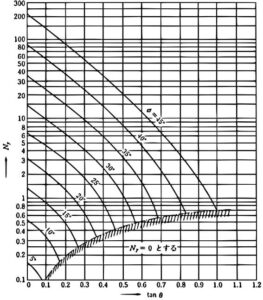
\(N_c, N_q, N_γ\)は、地盤の内部摩擦角φおよび基礎の傾斜角θを用いて、グラフから求めます。
ここに、基礎の傾斜は次式により計算するものとします。
$$tanθ=\frac{H_B}{V}$$
$$V:基礎底面に作用する鉛直荷重(kN)$$
$$H_B:基礎底面に作用する水平荷重(kN)$$
支持力係数\(N_c, N_q, N_γ\)は、地盤のせん断破壊を前提としてテルツァーギの支持力公式を傾斜荷重に対して拡張したものです。
グラフから、同一の地盤(同じ内部摩擦角φ)の直線についてみると、傾斜(tanθ)が大きくなるにつれて\(N_c\)が小さくなっているのが読み取れます。
これは、基礎が傾いていると支持力は小さくなるという実現象を再現しています。
tanθが極度に大きい領域についてはグラフに表示されていませんが、基礎の傾斜が大きい場合にはほとんど支持力を発揮できなくなるため、支持力係数\(N_c=0\)として計算を行うことになります。\(N_q, N_γ\)も同様です。
\(S_c, S_q, S_γ\):寸法効果にかかる係数
\(S_c, S_q, S_γ\)は支持力係数の寸法効果に関する補正係数で、次式の通り求めます。
\[
\left.
\begin{array}{l}
S_c&=(c^*)^{-1/3}\\
S_q&=(q^*)^{-1/3}\\
S_γ&=(B^*)^{-1/3}
\end{array}
\right\}
\]
ここで、
$$c^*=\frac{c}{10} (1≦c^*≦10)$$
$$q^*=\frac{q}{10} (1≦q^*≦10)$$
$$B^*=\frac{B}{1.0} (1≦B^*)$$
ここで、c:地盤の粘着力(kN/m2)、q:上載荷重(kN/m2)、B:基礎の有効幅(m)です。
以上、今回は直接基礎の支持力公式について、テルツァーギの支持力公式から拡張に至る導出過程と各項の意味を解説しました。
べた基礎、布基礎、クレーン基礎等、直接基礎の支持力検討にぜひ役立ててください。

