単純梁とは、水平部材の両端をピン支持(水平解放)した構造を指します。
構造力学で習う中で、もっともポピュラーな形です。
計算が簡単というメリットを活かして、実際の設計でも大半が単純梁モデルで計算されています。
実例は後述します。
単純梁の曲げモーメント公式
先に公式を見ておきましょう。
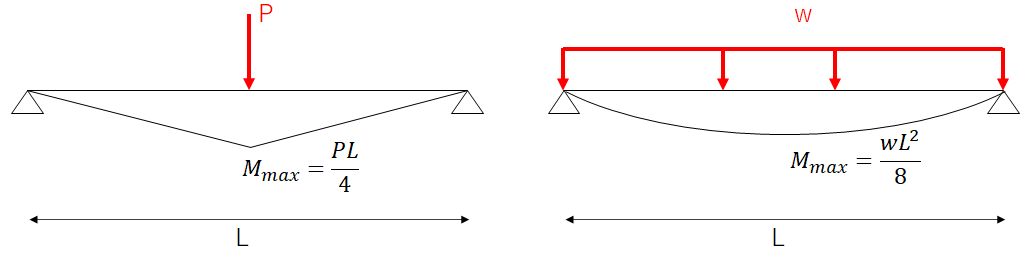
曲げモーメントは荷重とスパン長に比例します。
分布荷重の場合もwl=Pとみなすと、荷重とスパン長に比例していることがわかりますね
一方で、wl=Pとみなした場合、分母が異なりますよね?
集中荷重の場合はPL/4、分布荷重の場合はPL/8と解釈できます。
すなわち、同じ荷重なら分布荷重の方が曲げモーメントが小さくて済みます。
曲げが大きいと部材に働く応力が大きくなり壊れやすくなるので、できるだけ小さくするため分布荷重にするのがベターです。
工事現場に鉄板が敷いてあるのをよく見かけますよね?
あれは重機のタイヤが集中荷重なので、敷鉄板など面上のものを挟むことで地面にかかる力を分散させているのです。
単純梁のたわみ公式
たわみは次式で求めます。
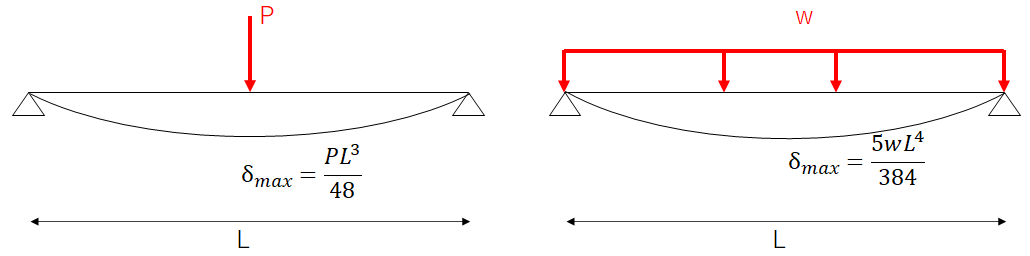
wl=Pとすると1/48>5/384より、たわみについても分布荷重の方が小さく済むことが分かりますね。
単純梁を使った実例としては、覆工板があります。
覆工板は、道路下を掘削して工事する場合に、その天井としてかつ路面として機能します。
覆工板は車両の走行に対しては安全なようにメーカー側で設計されているのですが、クレーンなどの重機が乗る場合には曲げモーメントが過大になるので、覆工板の上に鉄板を敷くことでクレーン荷重を鉄板の面積に分散させる対策が取られることが多いです。
特に覆工板や橋梁など車両が乗る構造物の場合には段差ができると車が走れなくなってしまうため、たわみ量が重要視されます。
以上今回は構造設計の基本となる単純梁について解説しました。
載荷位置や台形分布荷重時のモーメントなども公式化されていますので、ぜひ調べてみてください。

