チャン(chang)の式とは
一般に杭はその下端が土中に位置し、回転が自由です。
また、作用する外力の大きさによって、どこまでが変形し、どこからが変形しない固定端となるのかが変化します。
そのような条件から、杭に発生する断面力(曲げモーメントやせん断力)の計算は非常に難解です。
ではどのようにして杭の曲げモーメントを計算しているのでしょうか?
一般的に使用される道路橋示方書では、杭に発生する断面力の計算に「チャンの式」という公式を採用しています。
チャンの式の公式は記事の後半にありますので、解説不要な方は後半まで飛ばしてチェックしてください。
有限長の杭・半無限長の杭の違い
チャンの式では、「有限長の杭」「半無限長の杭」という区分けを行うことで複雑な杭問題を公式化することに成功しています。
杭長による公式の場合分け
杭長が無限に長い杭を考えます。
杭上端に水平方向の外力が作用し、杭が曲がっています。
この場合、杭の曲がり、すなわち曲げモーメントや変位に対して、無限に深い位置にある杭先端(杭下端)は影響をほとんど与えないことは容易に想像できますよね。
一方で、杭長が短い場合には杭先端(杭下端)の固定条件に影響されることも想像に難くありません。
したがって、チャンは、杭長がある長さよりも短い場合には、杭先端の条件(自由端・ヒンジ・固定端)ごとに計算式を用意しています。
一方で杭長が十分に長い場合には、杭先端の条件によらず同じ式としています。
ただし、半無限長の杭の場合にも杭頭部が突出しているかどうかで式が場合分けされています。
まとめると、有限長の杭とは、発生断面力が杭先端の影響を受ける杭であり、半無限長の杭とは、杭先端の影響が無視できるほど小さい杭を意味します。
有限長・半無限長の区分け基準
有限長の杭と半無限長の杭を分ける基準となる長さは、次式で計算できます。
\(βL_e<2.5\):有限長の杭
\(βL_e≧2.5\):半無限長の杭
杭長\(L_e\)が2.5/βよりも小さい場合には杭先端の影響が大きいことが経験的にわかっているため、上式のような区分けになっています。
また、βは杭の特性値と呼び、単位は(\(mm^{-1}\))です。
チャンの公式一覧表
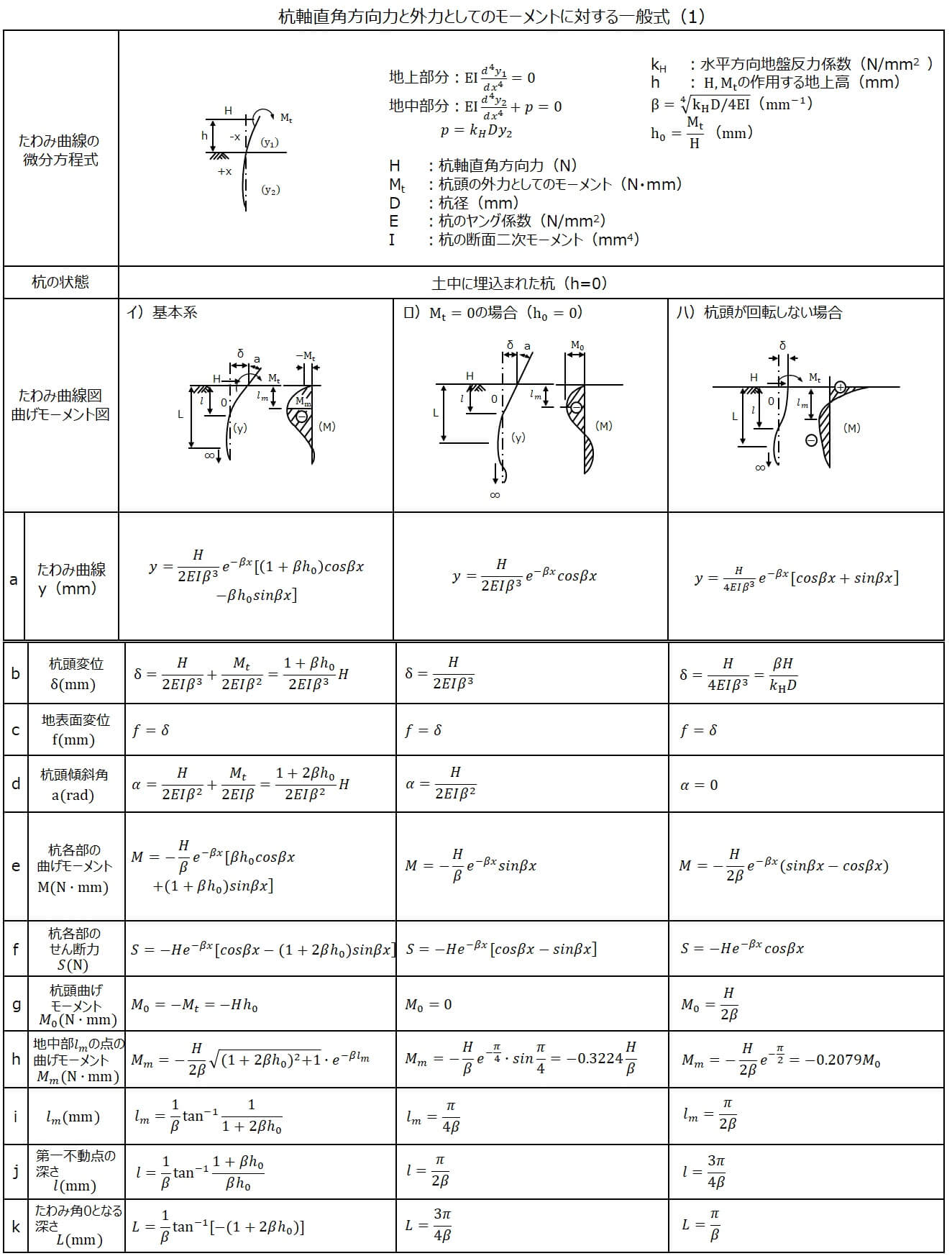
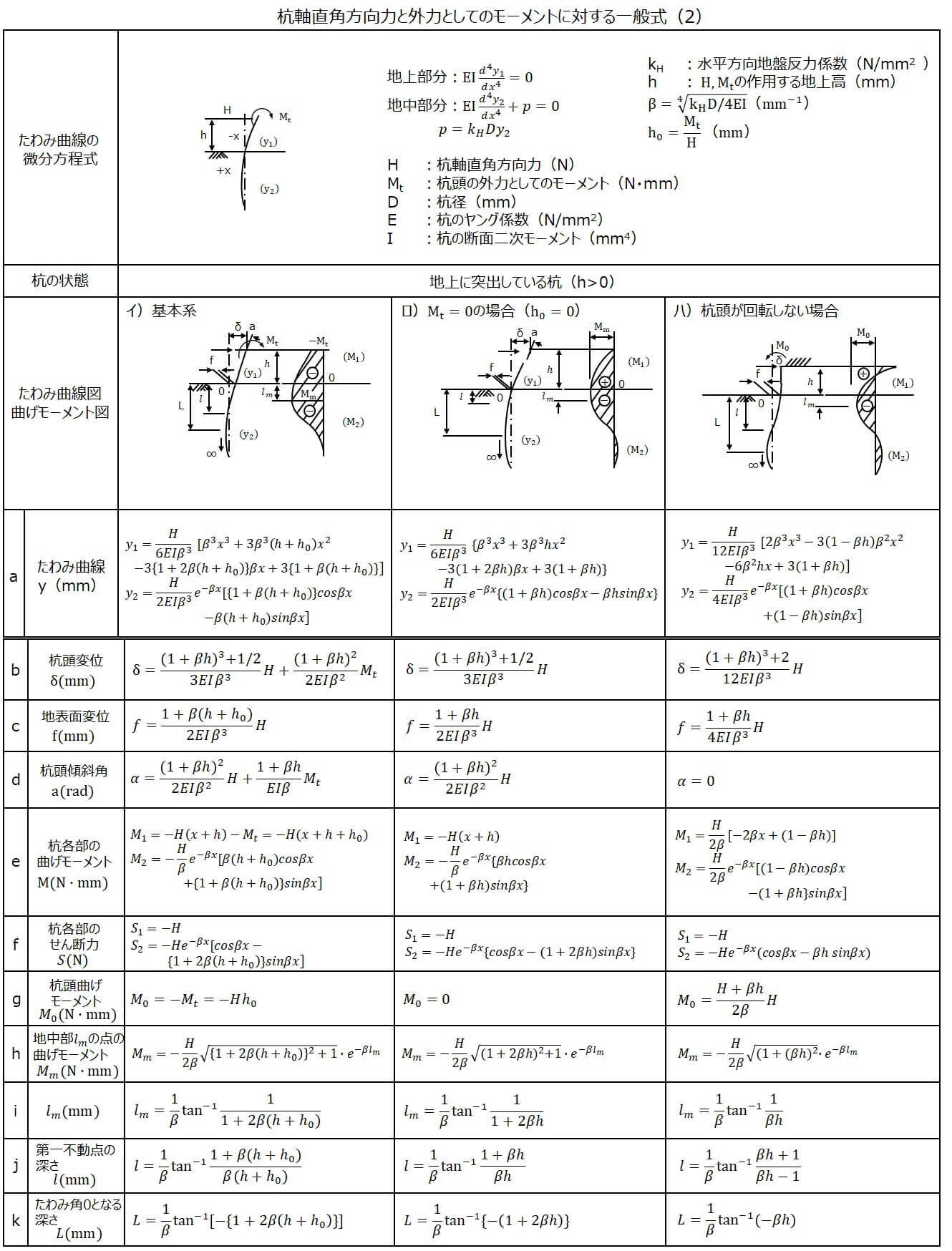
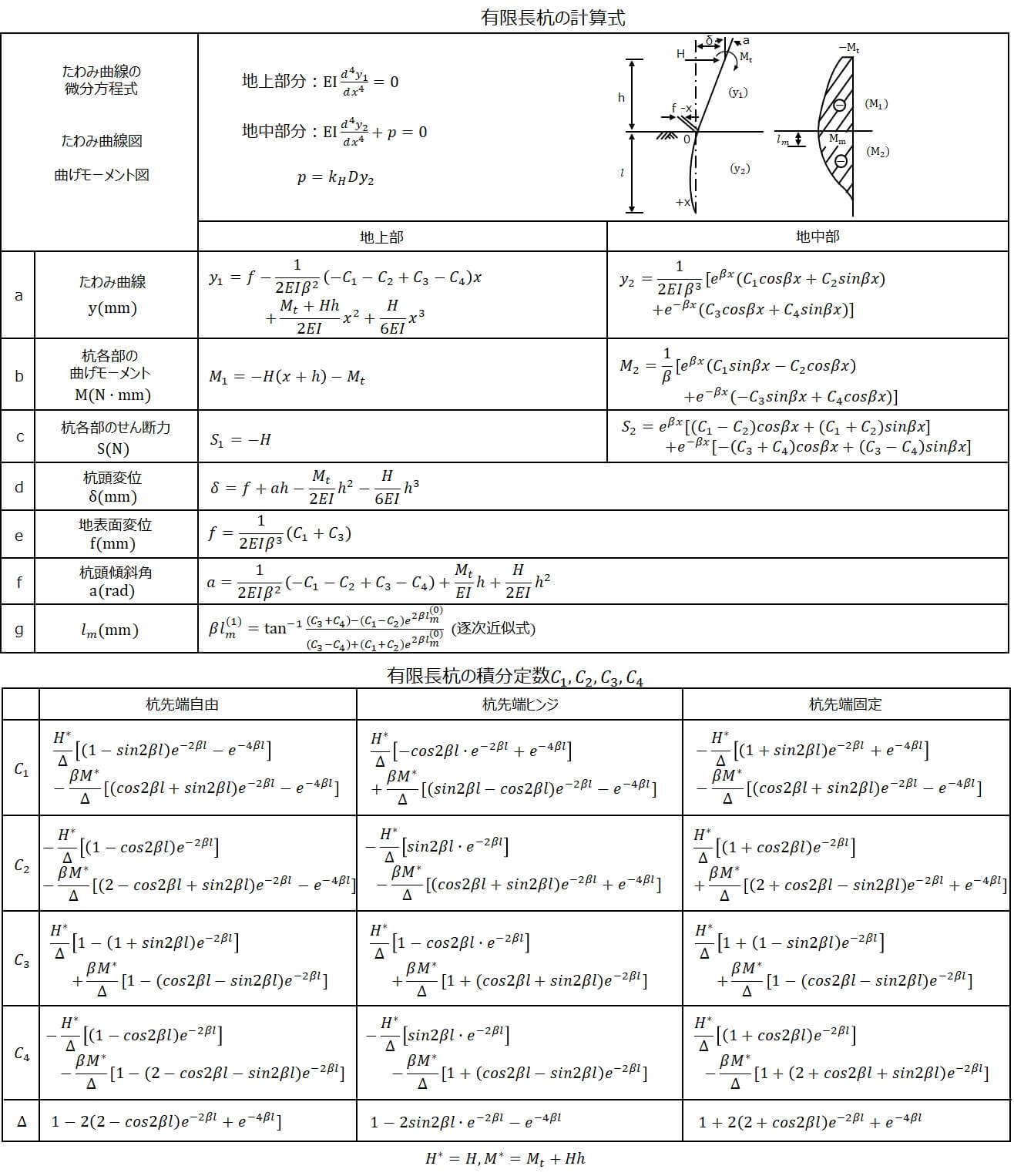
有限長の杭の公式の導出
有限長の杭の公式は次式を用いて導出されています。
地上部のたわみ曲線:
$$y_1=α_1x^3+α_2x^2+α_3x+α_4$$
地中部のたわみ曲線:
$$y_2=exp(βx)(C_1cosβx+C_2sinβx)+exp(-βx)(C_3cosβx+C_4sinβx)$$
ここで、\(α_1~α_4\)、\(C_1~C_4\)は以下の境界条件から算出して用います。
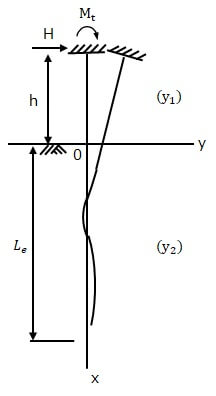
杭頭条件:
\begin{eqnarray}
\left\{
\begin{array}{l}
EI[y_1^{(3)}]_{x=-h}=H \\
EI[y_1^{(2)}]_{x=-h}=M_t
\end{array}
\right.
\end{eqnarray}
x=0における連続条件
\begin{eqnarray}
\left\{
\begin{array}{l}
[y_1]_{x=0}=[y_2]_{x=0} \\
[y_1^{(1)}]_{x=0}=[y_2^{(1)}]_{x=0}\\
[y_1^{(2)}]_{x=0}=[y_2^{(2)}]_{x=0}\\
[y_1^{(3)}]_{x=0}=[y_2^{(3)}]_{x=0}
\end{array}
\right.
\end{eqnarray}
杭先端の条件によって下記の中から1つ選択して用います。
杭先端自由:
\begin{eqnarray}
\left\{
\begin{array}{l}
[y_2^{(2)}]_{x=L_e}=0 \\
[y_2^{(3)}]_{x=L_e}=0
\end{array}
\right.
\end{eqnarray}
杭先端ヒンジ:
\begin{eqnarray}
\left\{
\begin{array}{l}
[y_2]_{x=L_e}=0 \\
[y_2^{(2)}]_{x=L_e}=0
\end{array}
\right.
\end{eqnarray}
杭先端固定:
\begin{eqnarray}
\left\{
\begin{array}{l}
[y_2]_{x=L_e}=0 \\
[y_2^{(1)}]_{x=L_e}=0
\end{array}
\right.
\end{eqnarray}
以上、有限長の杭、及び半無限長の杭に発生する断面力を求めるチャンの式を解説しました。

